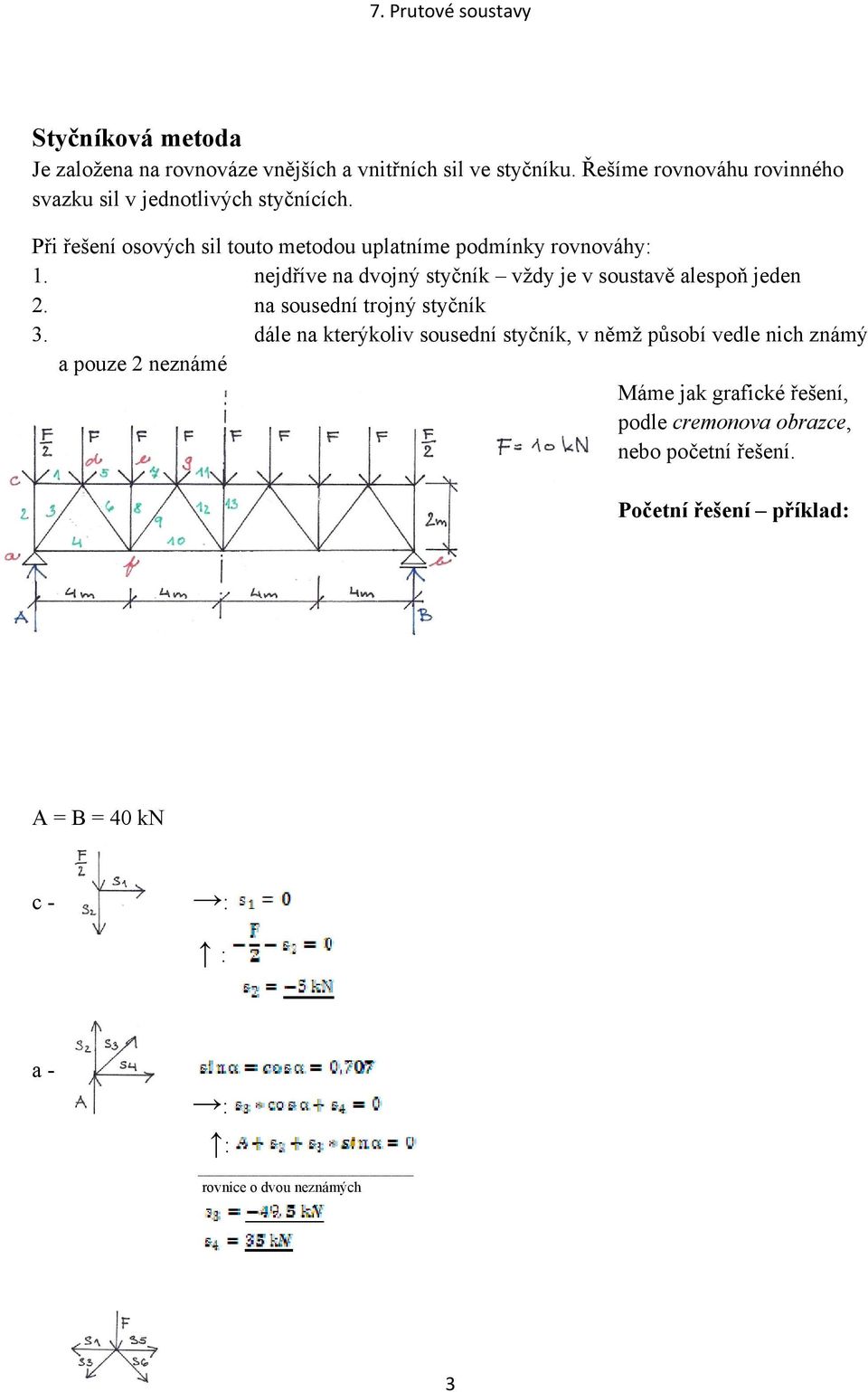
Při použití této metody nejprve nahradíme všechny pruty konstrukce normálovými silami, jejichž směr volíme ven ze styčníku. Předpokládáme, že všechny pruty budou namáhany tahem. Výjde-li při výpočtu u některé normálové síly záporné . Podmínky rovnováhy v jednotlivých styčnících řešíme místo graficky početně. Jsou to síly působící v jednom bodě, máme tedy k dispozici dvě podmínky rovnováhy (∑Fix = ∑Fiy = 0).
U neznámých sil v prutech předpokládáme, že jsou tahové, když vyjdou záporně, budou tlakové.
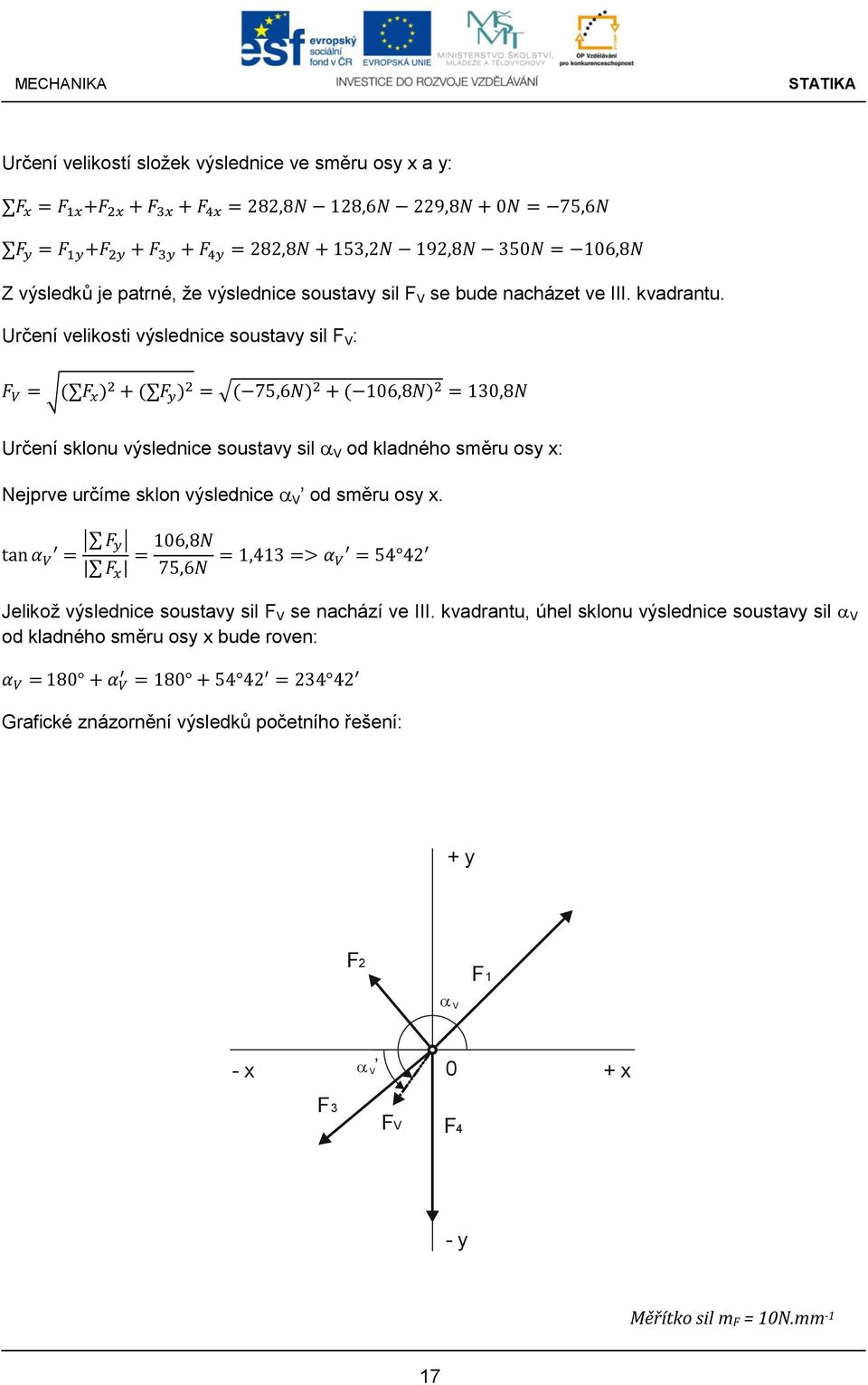
Otázky spojené s problematikou dimenzování posléze řeší nauka o pružnosti a pevnosti. Grafické řešení reakcí na prutové konstrukci. Při řešení této úlohy početní metodou , vycházíme z podmínek rovnováhy. Silové účinky jsou zakresleny na obr.
Smysl reakčních sil je předpokládaný a vychází ze síly zátěžné. V jednom styčníku se vždy stýkají nejméně dva pruty. Příklad: Určete početní metodou velikost osových . Proto musíme při výpočtu postupovat tak, abychom stále řešili pouze ty styčníky , ve kterých jsou nejvýše dvě neznámé síly v prutech.
Zjistíme, zda příhradová konstrukce je staticky i tvarově určitá.

Jedná se o grafické řešení prutové soustavy. Pro tento typ řešení potřebujeme schéma prutové soustavy v měřítku, vedle kterého budeme vynášet složkový obrazec. Styčníková metoda a Cremonův diagram. Inovace a zkvalitnění výuky prostřednictvím ICT.
Název: Mechanika, statika. Téma: Prutové soustavy početní řešení. Z toho je zřejmé, že řešit lze jen takové styčníky , kde kromě známých sil jsou nejvíce dvě síly neznámé.
Početní řešení rovinných prutových soustav. Později dimenzovat nebo kontrolovat pevnost prutů a styčníků. Celkovým obrazcem podle Cremona. Podstatou grafického řešení je to, že všechny síly . Očíslovat styčníky a pruty.
Zkontrolovat statickou určitost. Vypočítat reakce na podpěrách. Vychází z grafického řešení, kdy velikost sil počítáme z jednotlivých styčníkových trojúhelníků nebo mnohoúhelníků pomocí geometrických funkcí . Základní rozdělení těchto metod je na grafické a početní. V současné době se prutové soustavy řeší převážně početně a to buď obecnou, nebo postupnou styčníkovou metodou.
Metody řešení prutových soustav. Všechny styčníky se uvolní najednou a pro každý se .
Obecná styčníková metody. FliegenderZirkus: mohl bych poprosti jestli bsjte mě nespočítal aspoň pruty , , ? Kontrola: Poznámka: Výpočet posledního styčníku má kontrolní charakter. Drobná nepřesnost je dána zaokrouhlením v dílčích výpočtech. Potvrzením správnosti řešení je souhlas výsledků získaných grafickou metodou (vše je třeba narýsovat v měřítku) s výsledky získanými metodou početní.
Matematický model, princip výpočtu. Počítáme tak, že všechny pruty jsou dokonale tuhé, všechny styčníky dokonalé klouby a podpěry.